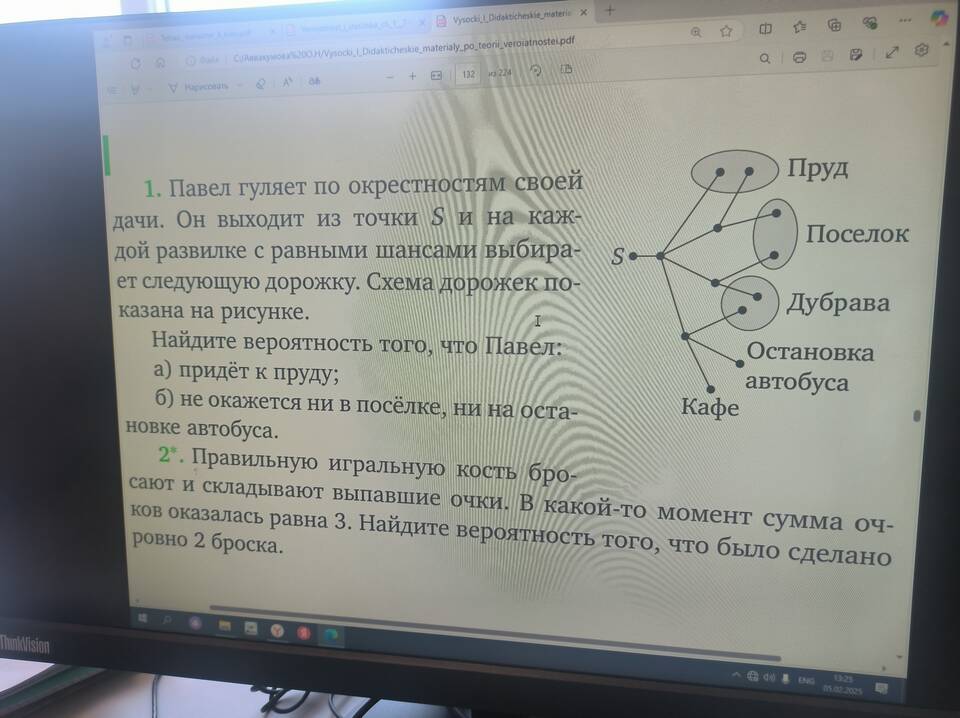
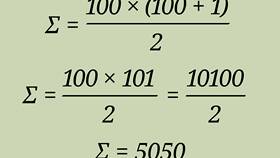В теории вероятностей сумма вероятностей всех возможных исходов эксперимента всегда равна единице. Это фундаментальное свойство имеет глубокое математическое обоснование и практическое значение.
Содержание
В теории вероятностей сумма вероятностей всех возможных исходов эксперимента всегда равна единице. Это фундаментальное свойство имеет глубокое математическое обоснование и практическое значение.
Аксиоматическое обоснование
- Первая аксиома Колмогорова: вероятность любого события неотрицательна
- Вторая аксиома: вероятность достоверного события равна 1
- Третья аксиома: вероятность суммы несовместных событий равна сумме их вероятностей
Математическая интерпретация
| Свойство | Формулировка |
| Нормировка | ∑P(ωi) = 1 для всех ωi∈Ω |
| Полная группа | События покрывают все возможные исходы |
Практическое объяснение
- Вероятность измеряет степень уверенности в наступлении события
- Сумма всех возможных исходов представляет полную уверенность (100%)
- Единица выступает как максимально возможное значение вероятности
- Это соглашение позволяет стандартизировать расчеты
Пример с игральной костью
| Исход (выпавшее число) | Вероятность |
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
| Сумма | 6/6 = 1 |
Значение этого свойства
- Позволяет проверять корректность распределения вероятностей
- Служит основой для вычисления дополнительных вероятностей
- Обеспечивает согласованность теоретических моделей
- Дает возможность сравнивать разные вероятностные пространства
Равенство суммы вероятностей единице является краеугольным камнем теории вероятностей. Это свойство отражает полноту и непротиворечивость вероятностной модели, гарантируя, что учтены все возможные исходы эксперимента.
