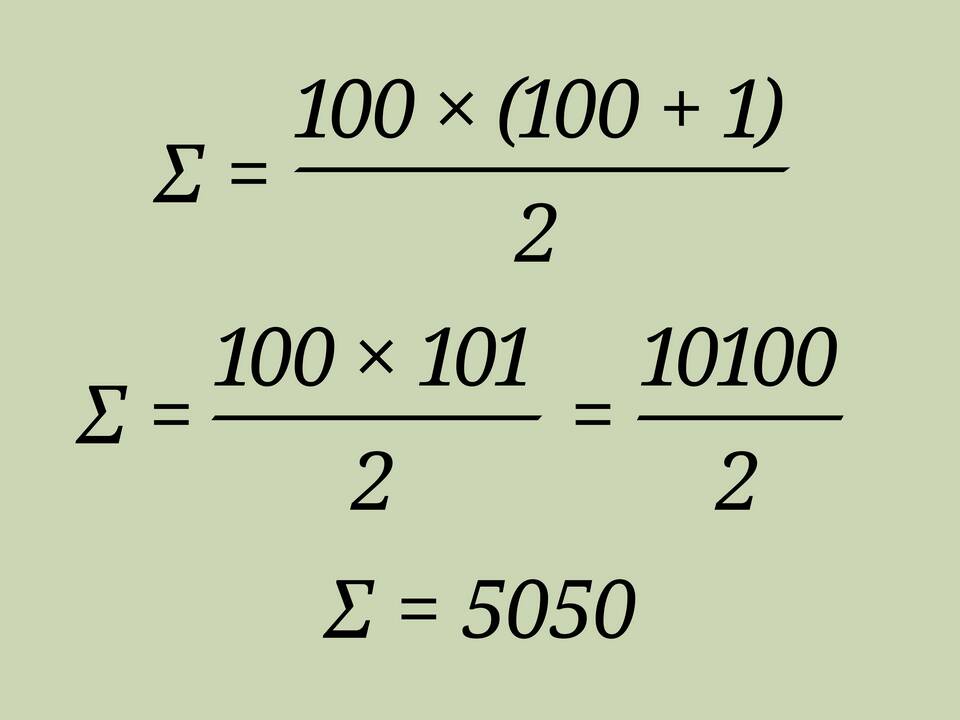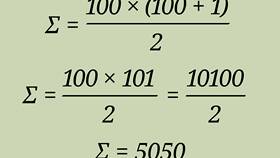Вопрос о сумме всех четных чисел приводит к интересным математическим концепциям и парадоксам. Рассмотрим эту проблему с точки зрения современной математики.
Содержание
Сумма четных чисел в конечном диапазоне
Для конечного набора четных чисел их сумма всегда определена и конечна. Например:
| Диапазон | Сумма четных чисел |
| От 2 до 10 | 2 + 4 + 6 + 8 + 10 = 30 |
| От 1 до 100 | 2550 |
Бесконечный ряд четных чисел
При рассмотрении бесконечного ряда четных чисел (2, 4, 6, 8, ...) возникают следующие особенности:
- Ряд является строго возрастающим
- Каждое последующее число на 2 больше предыдущего
- Сумма членов ряда стремится к бесконечности
Математическая интерпретация
Сумма бесконечного ряда четных чисел расходится:
- Частичные суммы неограниченно возрастают
- Не существует конечного предела последовательности частичных сумм
- По определению, такой ряд считается расходящимся
Сравнение с суммой натуральных чисел
| Характеристика | Четные числа | Все натуральные числа |
| Рост элементов | +2 на каждом шаге | +1 на каждом шаге |
| Сумма первых n членов | n(n+1) | n(n+1)/2 |
| Поведение при n→∞ | Стремится к +∞ | Стремится к +∞ |
Парадоксальные свойства
Несмотря на то, что четные числа составляют лишь часть натуральных:
- Мощность множества четных чисел равна мощности множества всех натуральных чисел
- Оба множества являются счетными
- В теории множеств они считаются "равными по размеру"
Таким образом, сумма всех четных чисел в бесконечном ряду формально равна бесконечности, как и сумма всех натуральных чисел, хотя интуитивно может казаться, что сумма четных чисел должна быть "меньше".