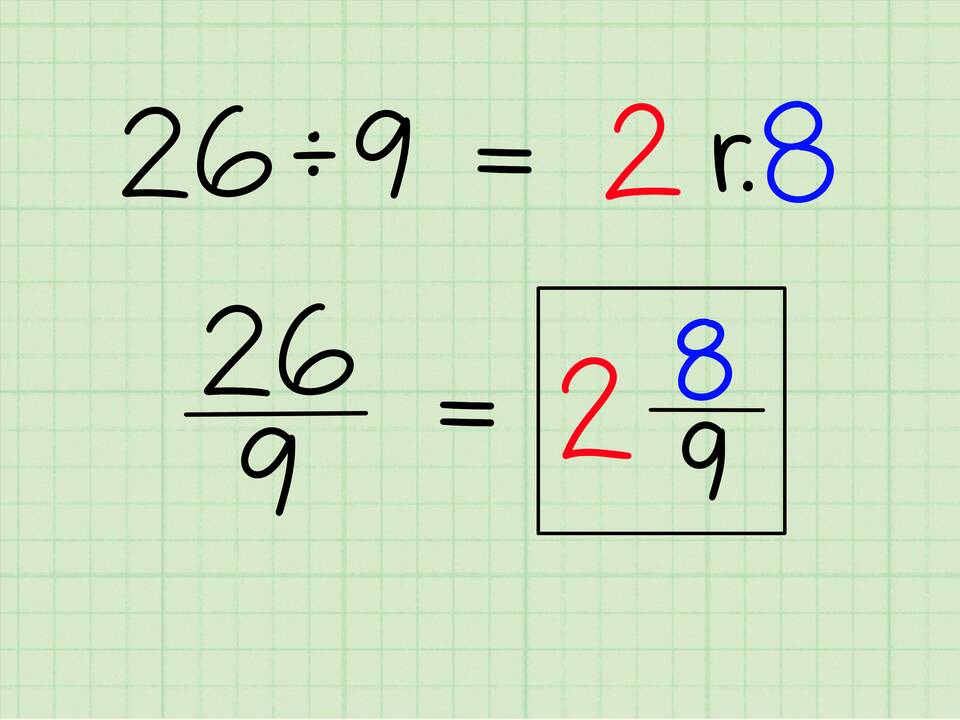Сложение смешанных дробей требует выполнения последовательности математических операций. Рассмотрим пошаговый метод вычисления суммы смешанных чисел с примерами и пояснениями.
Содержание
Основные понятия
| Термин | Определение |
| Смешанная дробь | Число, состоящее из целой части и правильной дроби |
| Правильная дробь | Дробь, где числитель меньше знаменателя |
| Общий знаменатель | Наименьшее общее кратное знаменателей |
Алгоритм сложения смешанных дробей
Пошаговая инструкция
- Сложите целые части смешанных чисел
- Приведите дробные части к общему знаменателю
- Сложите числители дробных частей
- Если дробная часть стала неправильной - выделите целое
- Добавьте выделенное целое к сумме целых частей
- Запишите итоговую смешанную дробь
Пример расчета: 2⅓ + 1¾
- Шаг 1: 2 + 1 = 3 (целые части)
- Шаг 2: ⅓ = 4/12, ¾ = 9/12 (общий знаменатель 12)
- Шаг 3: 4/12 + 9/12 = 13/12
- Шаг 4: 13/12 = 1¹⁄₁₂ (выделение целого)
- Шаг 5: 3 + 1 = 4 (итоговая целая часть)
- Шаг 6: Итог: 4¹⁄₁₂
Особые случаи сложения
| Ситуация | Решение |
| Разные знаменатели | Приведение к наименьшему общему знаменателю |
| Неправильная дробь в результате | Выделение целой части из дроби |
| Сложение с целым числом | Целое число преобразуется в дробь с знаменателем 1 |
Проверка правильности вычислений
- Преобразуйте смешанные дроби в неправильные
- Выполните сложение неправильных дробей
- Преобразуйте результат обратно в смешанную дробь
- Сравните с первоначальным результатом
Распространенные ошибки
- Сложение целых и дробных частей отдельно без приведения
- Ошибки в нахождении общего знаменателя
- Неправильное выделение целой части из дроби
- Потеря знаменателя при сложении числителей
Практические примеры
| Пример | Решение |
| 3½ + 2¼ | 5¾ |
| 1⅔ + 4⅚ | 6½ |
| 5¾ + 2⅛ | 7⅞ |